你有聽過「棉花糖實驗」嗎?這是史丹佛大學研究人員設計的一個心理學實驗,在一個小房間內,給小孩一顆棉花糖,並告訴他若15分鐘後棉花糖還在,就再給他一顆,然後研究人員離開房間,留下小孩一個人,並在房間外觀察小孩。
實驗發現,沒有吃掉棉花糖的小孩,長大以後的成績表現與身體健康,都比吃掉棉花糖的小孩要好。那你有沒有想過,存錢跟棉花糖實驗有關?
一寸光陰一寸金:貨幣時間價值
在「棉花糖實驗」中,如果忍耐了15分鐘,卻不會多一顆棉花糖做為獎賞,應該沒有小孩願意等吧?
存錢是犧牲了現在用這筆錢來消費享樂的滿足感,以換取未來更多的金錢。再加上,通貨膨脹也會讓未來的100塊錢能買到的東西變少,所以現在的100塊錢,會比未來的100塊錢還要值錢。
現值、未來值
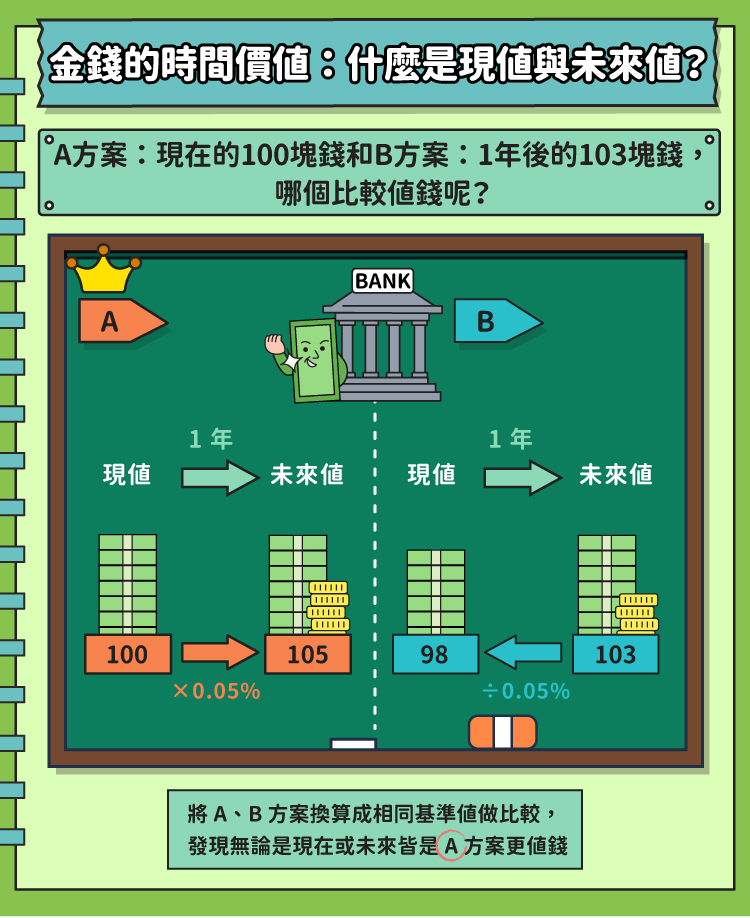
那麼,A方案:現在的100塊錢和B方案:1年後的103塊錢,哪個比較值錢呢?要解答這個問題,我們需要有如何計算現值、未來值的概念。
假設銀行存款提供5%的年利率。如果我們選了A方案,拿到100塊錢存到銀行裡,1年後你的存款會成長到105塊錢。所以,100塊在1年後的「未來值」,就是105。所以顯然,A方案:現在的100塊錢會比B方案:未來的103好,因為用未來值來比較,A是105,B是103。
我們也可以比較兩方案的「現值」。要知道B方案的現值,也就是1年後的103塊,現在值多少?這個問題相當於:現在要存多少錢,以銀行年利率5%,在一年後才會有103塊?1年後的103塊在還沒算利息之前,大概是98元(103 / (1+5%) = 98)。也就是說,B方案的現值大約為98。顯然A方案:現在的100塊會比B方案好,因為用現值比較,A是100,B約是98。
計算時間價值的方式:單利、複利
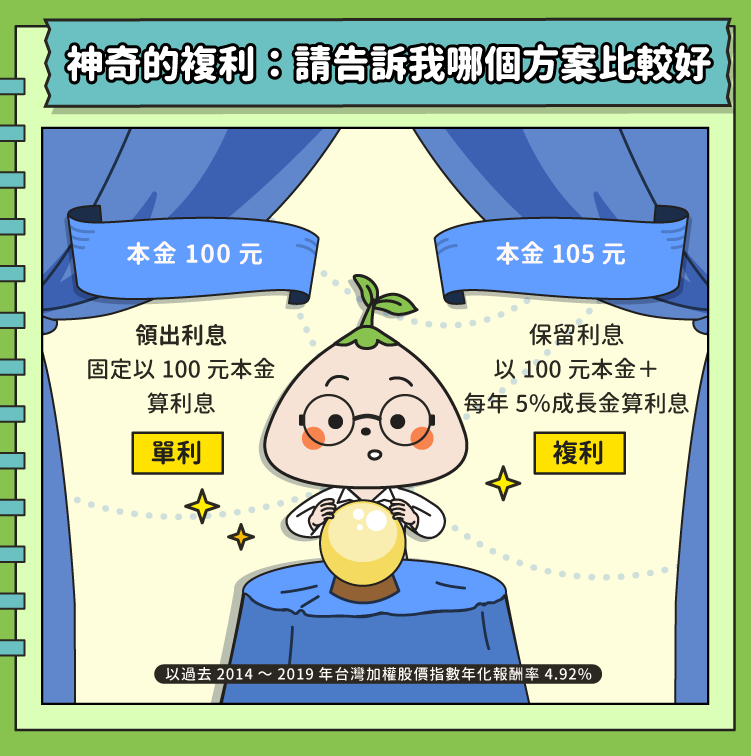
根據是否將獲得的報酬繼續投入,利率可以分成單利、複利。以上面的例子來說,假設在第一年,我的100塊錢以5%年利率成長後變成105塊,我把5塊拿出來買棉花糖,剩下的100塊繼續存,這5塊就不會隨著100塊的本金繼續算利息。這就是只有本金會算利息的「單利」。
如果我在第一年結束時,忍住吃棉花糖的衝動,這5塊就隨著100塊本金繼續滾利息,下一年算利息的基礎就是105,這就是「複利」。
七二法則
複利和單利的差別,可以用以下例子來看。今天我投入了100元,以年利率5%複利,幾年後我的資產會翻倍?最笨的方法,可以按計算機,100*(1+5%),一直乘105%,按到計算機顯示出200為止,看乘了幾次,就是需要的時間。要按14次才會接近200。
數學上有一個概算的方法叫做72法則:以X%的年利率複利計算,72 / X 年後,你所投資的金額會成長到2倍大。以上述的例子,72/5=14.4,也就是資產翻倍的時間約要14年;而如果用單利,每年利息5元領出來,則需要20年的時間才能累積到100塊,資產才能翻倍。6年的差距,這就是複利比單利強大之處。
利用複利為你創造財富
愛因斯坦曾說:「複利是世界第八大奇蹟」。你有想過七大奇蹟是哪七大嗎?
好這不重要,重要的是複利的威力。投資就像滾雪球,雪球黏起坡道上的濕雪變大,有更多表面積,去黏起更多坡道上的濕雪,這個過程一直循環,雪球變大的速度愈來愈快。複利也是一樣,利息滾入後,用來複利的金額會愈來愈大,因此利息會愈來愈多,又滾入本金複利,如此循環,資產就成長的愈快。
因此,不能小看複利的力量,及早規劃投資理財,透過長時間複利,一步一腳印累積財富,以錢滾錢,終會創造理想的財富。
【延伸閱讀】