在國際政治與貿易談判中,雙方如何在僵持不下的情況下選擇是否妥協?當兩國都處於極端對抗,互相施壓,誰會首先讓步?膽小鬼賽局正是這樣一場博弈,雙方不僅要衡量自己的損失承受能力,還要精準預測對方的反應。在這篇文章中,我們將探索膽小鬼賽局如何在歷史的關鍵時刻,如古巴危機與中美貿易戰中發揮作用?雙方如何通過釋放威脅、測試對方底線來達成妥協或繼續對抗?這場博弈,誰又能在最關鍵的時刻掌握主動權?讓我們一探究竟!
膽小鬼賽局是什麼?
在國際政治或貿易談判中,雙方往往處於一種既想強硬又擔心對方不妥協的僵持局面。膽小鬼賽局正是這種情境的縮影,它揭示了在極端對抗中,雙方如何通過施壓與測試對方底線來尋求最終的妥協。接下來,我們將深入探討膽小鬼賽局的運作原理,並透過歷史上的經典案例,揭示這種賽局如何影響全球局勢與談判結果。
理論概述
膽小鬼賽局(Game of Chicken)是賽局博弈論中的一種模型,和經典賽局不同之處在於:雙方無法在模型中找到單一納許均衡(Nash Equilibrium),因此賽局會逐漸走向邊緣策略(brinkmanship)(提高威脅至災難邊緣,迫使對手屈服)。
白話來說,膽小鬼賽局中不存在「最佳解」,一方的策略行動將仰賴於另一方,因此每位參與者都會試圖表現得比對方更強硬,希望對方先讓步。問題在於,若雙方都不退讓,最終將造成對雙方都不利的結果,也就是雙輸情境。這類賽局常見於國際政治或貿易談判中,例如最經典的古巴危機、台海兩岸關係、南北韓關係等等。
賽車案例
還是搞不太懂膽小鬼賽局如何應用?讓股感以經典的賽車案例帶你實際走過一次賽局!在賽車案例中,假設有兩台賽車(甲、乙)面對面向對方疾駛而去,先掉頭轉走的即為膽小鬼,若雙方皆不退讓,將導致嚴重對撞車禍。因此,可以假設出以下 4 種情形:
| 賽車中的膽小鬼賽局 | |||
| 註:數字為選擇該策略所獲之利益大小 | 乙 | ||
| 轉彎 | 直行 | ||
甲 |
轉彎 | (2,2) | (1,4) |
| 直行 | (4,1) | (-2,-2) | |
- 純策略組合純策略組合
若雙方皆妥協轉彎,則雙方皆獲得中等利益;若一方轉彎一方直行,則一方獲最大利益,一方獲次差利益;若雙方皆選擇直行,則雙方將面臨最差利益。在這樣的局面中,存在著兩種納許均衡(雙方皆無動機改變目前策略,指目前策略為最佳選擇):甲直行乙退讓、乙直行甲退讓。以「甲直行乙退讓」來說,甲的利益大小為 4,沒有動機改為利益大小只有 2 的轉彎;乙的利益大小為 1,沒有動機改為利益大小只有 -2 的直行。
由此可知,雙方皆會想要獲得「自己堅持,對方退讓」的局面,然而出現兩種納許均衡的賽局是不穩定的,該如何確定在自己堅持的情況下,對方一定會妥協呢?這時我們可以加入妥協機率變數 p。
- 混合策略組合
假設我們是甲,則目標是算出要讓乙妥協,需要展現多少比例的轉彎/直行訊號,假設我們轉彎的機率為 p;直行機率為(1 – p)。下一步,我們需要計算乙兩種選擇的期望值:
- 轉彎期望值 = 甲轉彎情況+甲直行情況 = 2 x p + 1 x (1 – p) = p + 1
- 直行期望值 = 甲轉彎情況+甲直行情況 = 4 x p + -2 x (1 – p) = 6p – 2
要達成納許均衡,則要讓乙對兩種選擇感到無差異,讓乙認為其就算直行也不會得到更多利益,進而選擇較安全的轉彎。因此計算兩種情況期望值相等時的 p 值:
p + 1 = 6p – 2 ⭢ 5p = 3 ⭢ p = 3/5
由算式可知,若我們展現出 60% 的轉彎訊號及 40% 的直行訊號,能夠有效讓乙轉彎,進而獲得最大利益 4。這樣就達成了最理想的結果!不過,現實世界中的政治博弈往往更為複雜,接下來讓我們回顧最經典的古巴危機,一探利益與釋放訊號如何被實際計算。
古巴危機案例
古巴危機(Cuban Missile Crisis)發生於 1962 年 10 月,是美國與蘇聯之間最緊張的時刻之一。當時蘇聯在古巴部署了核導彈,引發美國的強烈反應,並決定對古巴進行海上封鎖。經過 13 天的緊張外交談判和軍事對峙,兩國最終達成協議,蘇聯撤回導彈,美國則承諾不入侵古巴,並秘密撤除在土耳其的美國導彈。這場危機展示了動態賽局中風險的變化與策略的應對,因而成為著名的膽小鬼賽局範例。
| 資料來源:“We haven’t got but one more day” The Cuban missile crisis as a dynamic chicken game;資料時間:2019/11 註:數據來自論文中假設,詳細計算過程見原文 |
|||
| 古巴危機中的膽小鬼賽局 | |||
| 蘇聯 | |||
| 撤除古巴導彈 | 保留古巴導彈 | ||
美國 |
海上隔離古巴 | (0,0) | (-1,1) |
| 空襲古巴 | (1,-1) | (C,C) | |
根據此篇論文假設,美蘇雙方各自有對於核戰的利益損害,而承受核戰損害的門檻將在談判過程中逐漸趨近於 0,若損害程度超過門檻,代表其會採取妥協策略。白話來說,損害程度越低(越趨近 0)的玩家能夠堅持越久。
從美國偵察機拍到蘇聯飛彈基地開始,雙方各自釋放許多堅持/妥協的訊號,一來一往中不斷增加核戰發生的機率,並降低承受核戰損害的門檻。以下列出幾個雙方曾釋放出的不確定性與訊號:
| 美蘇策略 | ||
| 妥協策略 | 堅持策略 | |
| 美國 |
|
|
| 蘇聯 |
|
|
而由下圖,我們可以發現以下關鍵重點:
- 發生核戰的機率在談判過程中從 1% 逐步提高至 75%,甚至在達成協議當天來到 100%,顯示若當天美蘇未達成協議,雙方將承受核戰帶來的災害。
- 美蘇對於核戰的損害程度應介於 -1 ~ -1.416 之間,顯示雙方的高耐受度。
- 在真實世界中,上下屬之間的分歧與意外可能導致局勢變動。例如:10 月 27 日一位較低位階的蘇聯軍官越過上級指示擊落美國飛機,加速古巴危機失控。
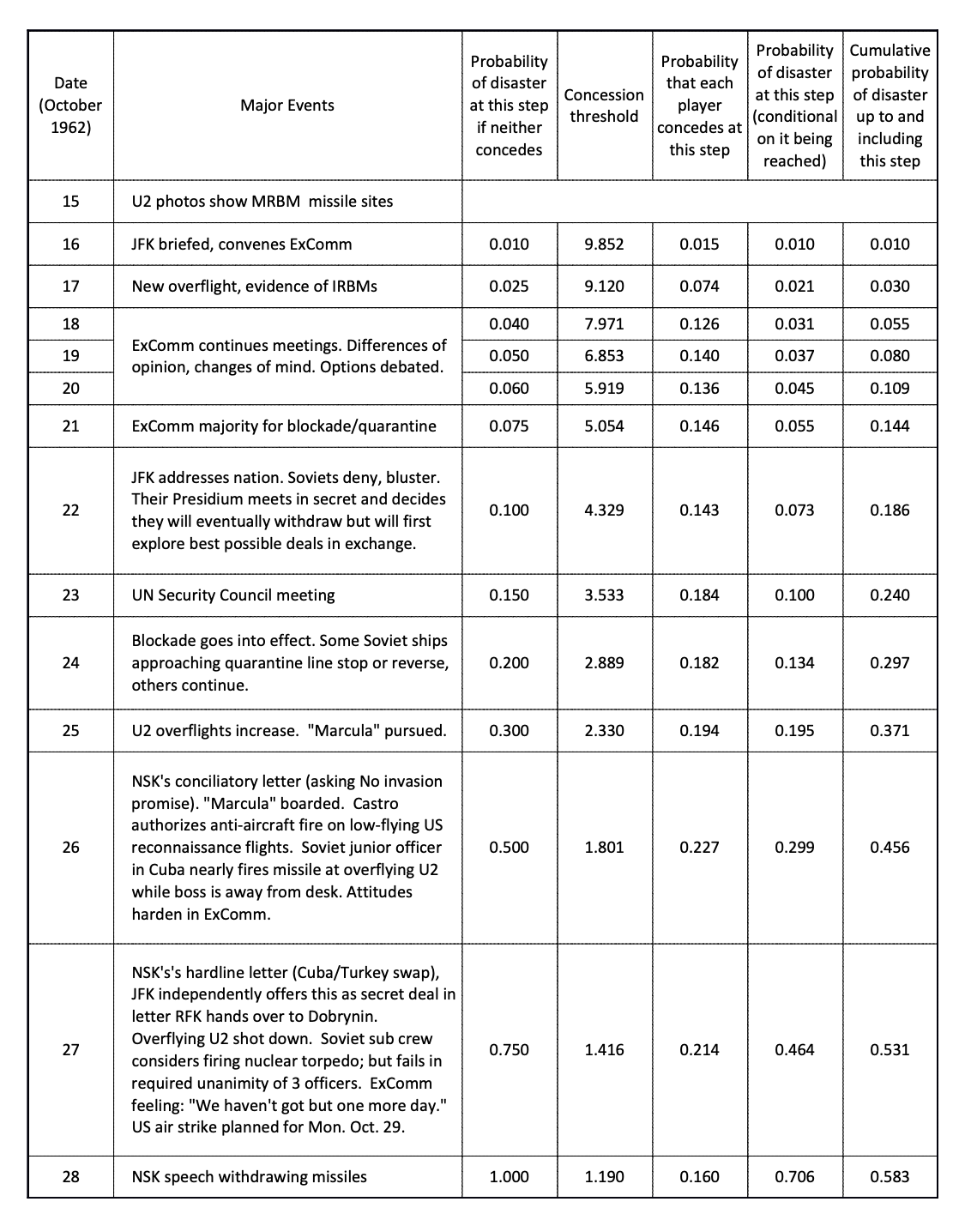
資料來源:“We haven’t got but one more day” The Cuban missile crisis as a dynamic chicken game;資料時間:2019/11
中美貿易戰中的膽小鬼賽局
目前中美局勢也處於膽小鬼賽局中,究竟貿易戰現況如何?雙方各自釋出多少妥協或堅持的策略?中美雙方的關鍵策略是什麼?中美貿易戰的發展為何?跟著股感一探究竟!
中美貿易戰現況
筆者整理自 4 月以來美中分別釋出的訊號,並依照膽小者賽局架構分類為妥協與堅持策略:
| 中美策略 | ||
| 妥協策略 | 堅持策略 | |
| 美國 |
|
|
| 中國 |
|
|
而根據 5 月 7 日所釋出的最新消息指出,美中將在 5 月 9 日至 12 日在瑞士舉行首次會談。願意進行面談與在第三方中立國舉行會談兩個關鍵,象徵雙方目前暫時處於合作(妥協,妥協)的次佳結果中。雖然根據美國財政部長貝森特所說:「我感覺這次會談重點會放在降溫,而不是那種大型貿易協議,我們不想脫鉤,我們要的是公平貿易。」預期關稅不會有重大變化,不過仍可視為貿易戰的一大推進,投資人可密切注意後續資訊!
編按:2025/05/13 更新,中美會談後,雙方均下調 115% 的稅率,顯示目前趨向於有限妥協策略。更詳細的關稅內容可以看這篇:中美達成關稅協議!川普關稅政策有哪些?為什麼要實施?對台灣有什麼影響?
中美策略關鍵
由於美中貿易戰已有川普上一任期的借鑑,我們可以套用日本學者藤本 悠雅(フジモト ユウマ)和金子 邦彦(かねこ くにひこ)所提出的概念,他們指出在動態賽局中,儘管雙方面對相同情況與規則,且皆會不斷學習、進化自己的策略,最終仍有一方能夠透過剝削(exploitation)贏得賽局。
而根據前一次貿易戰談判可知,美國相當在意通膨與終端消費。在上一次貿易戰中,美國核心的核心個人消費支出物價指數(Core PCE Price Index)皆維持在 2% 以內,且未直接對終端消費品課徵關稅。而此次川普雖直接全面課徵對等關稅,仍相當在意消費者感受。舉例來說根據新聞,亞馬遜曾預計要向消費者公開揭露關稅所造成的價格上升幅度,卻在川普政府施壓後,快速改口稱公開揭露關稅影響的計畫從未受到批准,也不會發生。
此外,川普能為所欲為的資本是美國目前強健的經濟數據表現,一旦通膨飆升、就業市場疲軟,民意可能反撲,將不利於中期選舉。因此,筆者認為美國的損害承受度關鍵在於,川普能夠接受經濟數據的反撲,以及終端消費品價格和供應鏈受到多大程度的影響。
而根據上一次中美貿易戰可知,中國不同於美國,比起通膨更在意「中國製造 2025」計畫,其中包括航太、精密器械、半導體等重點科技項目。根據下圖可知,中國雖在電子代工、消費性電子產品中擁有主導地位,當論及高階晶片處理,卻幾乎沒有市佔。由此可推論,中國在高階市場仍需依賴美國提供先進晶片。因此,筆者認為中國的損害承受度關鍵在於,其能承受科技、製造業在技術上受到多大程度的限制。
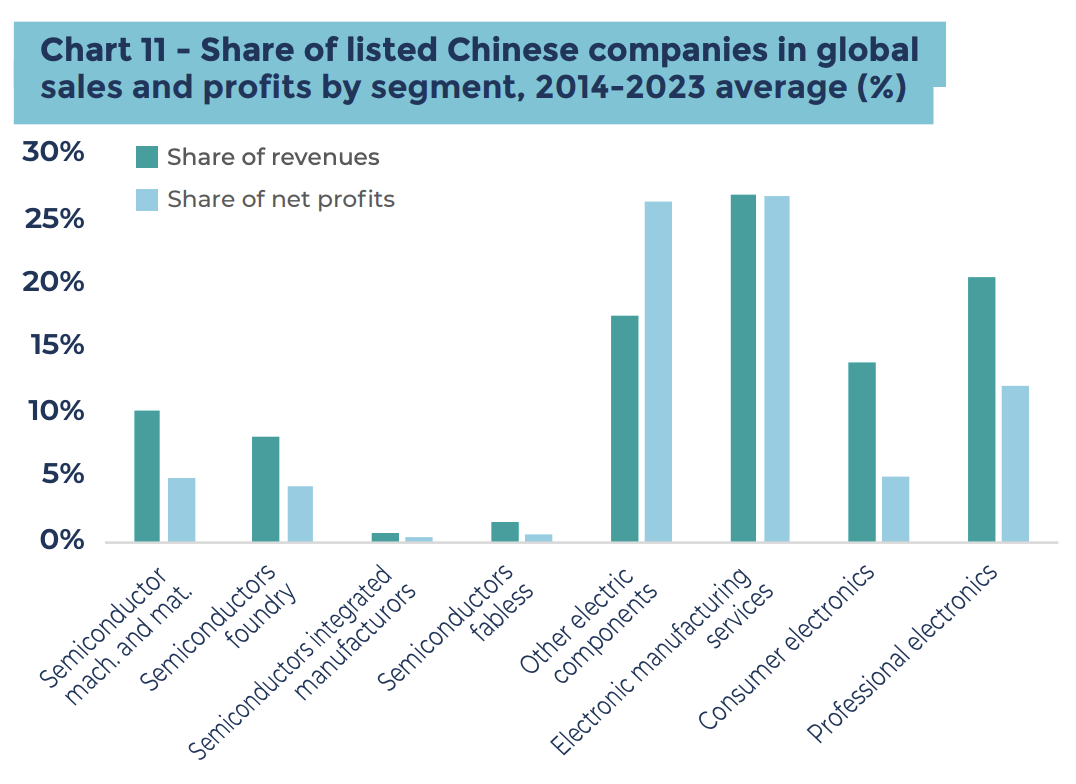
資料來源:Coface;資料時間:2024/11
未來發展
中美貿易戰未來走向可分為以下幾種劇本:
- 長期對立
不撤銷對等關稅,也就是維持現況,中美貿易活動將因高額關稅大幅減少,雙方需各自尋找新的供應鏈,而台廠有望因轉單受惠。
- 有限妥協
降低一定程度的關稅稅率,並報復特定產業,例如美國加大力度限制晶片出口中國、中國限制稀土等礦產出口美國等等。
- 完全和談
如同美國和其他國家進行的協談,雙方各自撤銷關稅,中美間貿易活動大幅增加,整體市場最大的不確定性也被消除。
而根據過去貿易戰的談判,及雙方領導人的強硬作風,筆者推測中美貿易戰將會走向長期對立與有限妥協。這場貿易戰最終考驗的將是,誰能釋出更多看起來「可信」的不確定性、展現出能承受更多損害的能力、在掌握大局風險的情況下,將對手步步進逼,使對手妥協的能力。
重點整理
- 膽小鬼賽局旨在透過不確定性與心理預期,迫使對手先妥協,成為「膽小鬼」
- 在膽小鬼賽局中,能承受更高強度損害、懲罰的玩家能留到最後
- 身處膽小鬼賽局,需辨明己方能承受的損害上限,與對方釋出訊號的可信度
- 中美貿易戰發展趨向長期對立與有限妥協
【參考資料】
- 膽小鬼賽局模型
- “We haven’t got but one more day” The Cuban missile crisis as a dynamic chicken game
- What is the best way to determine the optimal strategy in a game of chicken?
- Prisoner’s dilemma shows exploitation is a basic property of human society
- Exploitation by asymmetry of information reference in coevolutionary learning in prisoner’s dilemma game
【延伸閱讀】

