投資一間公司時,通常會使用本益比來判斷目前股價昂貴或便宜,然而在衡量成長股的股價時,應該使用本益成長比來評估,來選擇正確的進場時機。究竟本益成長比是什麼?怎麼算?如何用本益成長比選股?本篇文章帶你一探究竟!
本益成長比是什麼?
本益成長比(Price-to-Earning Growth Ratio,簡稱 PEG Ratio)是用來衡量「成長型股票是否昂貴或便宜」的指標,PEG 指標的創辦人為英國投資大師吉姆・史萊特(Jim Slater),隨後在美國傳奇投資人彼得・林區(Peter Lynch)的使用與推廣下,利用 PEG 選股才開始發揚光大。
一般而言,在判斷股價昂貴或便宜時,較常使用的指標為本益比,然而本益比僅考量了公司未來的獲利,而未考慮公司獲利的成長性,因此當一間企業處於快速成長時期,本益比就會偏高,使用本益比判斷就會認為其股價較昂貴,而使投資人錯失投資的機會,此時便可以使用本益成長比,將公司的未來成長性納入考量,協助投資人做出正確投資判斷。
💡延伸閱讀>>> 投資傳奇彼得林區:「這 7 種股票,我不買!」
PEG 計算公式
本益成長比(PEG)的計算方法是由「本益比」除以「盈餘成長率」所得的結果,其中「盈餘成長率」可以使用過去或預估未來的盈餘成長率進行計算,且建議以長期數據作為計算依據,例如:過去 5 年、未來 5 年等,其結果會較短期更為客觀準確。
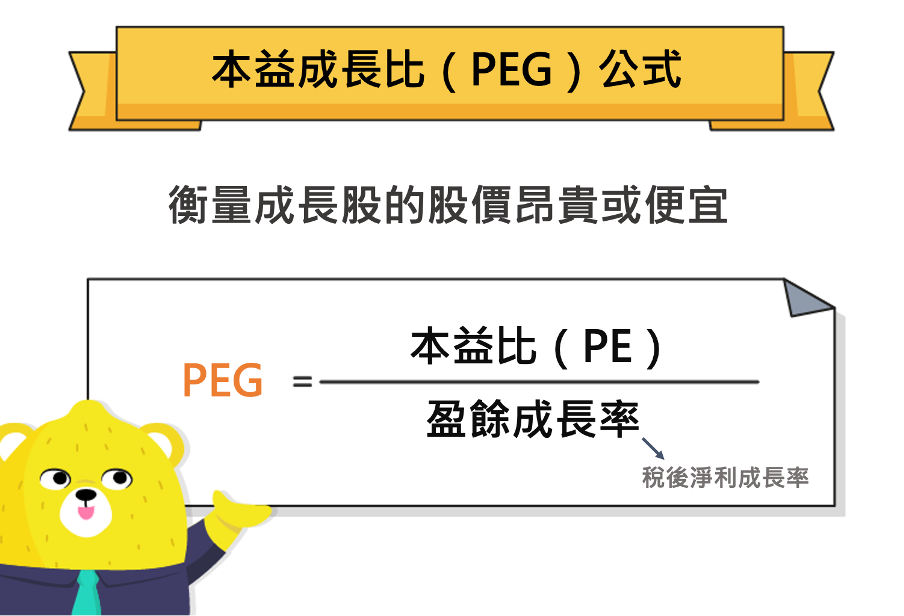
PEG 公式:本益成長比(PEG)=本益比(PE)÷ 盈餘成長率(稅後淨利成長率)
舉例:假設 A 公司目前股價 100 元,今年預估 EPS 為 10 元,預估稅後淨利成長率為 5% ,則 PEG=( 100 ÷ 10 )÷ 5 = 2 ,本益成長比為 2 (盈餘成長率以百分比 % 直接相除計算)。
💡延伸閱讀>>> 淨利是什麼?淨利率公式是?稅前淨利、稅後淨利差別在哪?
💡延伸閱讀>>> EPS 是什麼?怎麼用?EPS(每股盈餘) 提高股價就會漲?
PEG 查詢
瞭解 PEG 的計算後,除了可以自己用 PEG 計算公式計算,也可以將公司股價、每股盈餘、預估未來淨利年成長率輸入本益成長比計算機,即可算出個股的本益成長比,或至 Goodinfo!台灣股市資訊網的個股市況專區,輸入公司股票代碼即可查詢 PEG。
本益比 vs 本益成長比
- 本益成長比(PEG Ratio):衡量「成長型股票」是否昂貴或便宜的指標
- 本益比(PE Ratio):衡量股價是否昂貴與便宜的指標
本益比與本益成長比皆是衡量股價是否合理的指標,本益比僅考慮了公司的獲利,並未考量公司未來的成長性,而本益成長比則將獲利成長性納入衡量。當一間公司處於快速成長時期,使用本益比衡量可能會認為其股價昂貴,但若使用本益成長比則可以將公司成長性一併考慮,更能彰顯成長型公司的價值,然而沒有任何一項財務指標是可以完美詮釋公司的價值,因此在使用本益成長比時,仍應與其他指標搭配使用。
💡延伸閱讀>>>本益比是什麼?本益比怎麼算?本益比完整教學!
PEG 數值高低
PEG 指標的發明者吉姆・史萊特(Jim Slater)以本益成長比為 1 倍時,認為其股價為合理狀態,投資人應再行觀望;當本益成長比高於 1.2 倍時,認為其股價被高估,此時股價過於昂貴,投資人應進行賣出;當本益成長比低於 0.75 倍,甚至是低於 0.66 倍時,認為其股價被低估,此時股價過於便宜,投資人應進行買進。
| 本益成長比 PEG 評估標準 | ||
| 本益成長比(PEG) | 股價合理性 | 代表意義 |
| >1.2倍 | 高估 | 賣出 |
| =1倍 | 合理 | 觀望 |
| <0.75 倍(甚至<0.66 倍) | 低估 | 買進 |
| 資料來源:作者整理 | ||
本益成長比選股注意事項
在瞭解了本益成長比後,提醒投資人在使用本益成長比選股時應注意的事項,PEG 選股注意事項整理如下。
- 本益成長比(PEG)不是越小越好:本益成長比極小的特殊股票,有可能為短期內獲利起伏較大的公司,此類型公司股價波動大,投資風險可能較高。
- 本益成長比(PEG)要用來分析成長股:使用本益成長比的前提為公司是成長股,必須要公司當年度的本益比為正、EPS為成長,且成長率以較長期的數據作為依據,此時的本益成長比才會較有參考價值。
- 本益成長比(PEG)可能選到衰退的公司:任何財務數據皆為歷史數據,股價反映的是未來,且預估盈餘成長率並不簡單,投資人若無法根據多變的情況,改變對公司未來的預估,使用 PEG 選股還是可能選到衰退的公司。
- 本益成長比(PEG)可能錯失投資機會: 台股中許多股票 PEG< 0.75 倍或< 0.66 倍的時機並不多,若投資人堅持以 PEG 作為選股標準,可能錯失很多優良的投資標的,甚至比長期持有的報酬率更低。
- 本益成長比(PEG)建議搭配其他指標:投資人在選股時建議不要僅參考 PEG 指標,應該同時評估本益比、本益成長比,或其他財務指標,才能更全面的分析公司的投資價值。
PEG總結
- 本益成長比(PEG Ratio)是用來衡量「成長型股票是否昂貴或便宜」的指標。
- 本益成長比與本益比的差異在於對未來成長率的考慮,本益成長比將盈餘成長率納入指標中,更能彰顯成長股的價值。
- PEG 高於 1.2 倍時,代表股價高估應賣出;PEG 等於 1 倍時,代表股價合理應觀望;PEG 低於 0.75 倍或 0.66 倍時,代表股價低估應買進。
- 本益成長比不是越小越好,而且必須要是用來分析成長股。
- 使用本益成長比選股時建議搭配其他指標,且還是可能選到衰退中的公司,也有可能錯失投資機會。
【延伸閱讀】